#1 오일러각(Euler Angle)과 쿼터니언(Quaternions) 회전

matrix 변환 과정 중 rotation에 대해서는 이미 언급한적이 있다. 어떤 특정 하나의 축을 기준으로 회전시켰었다.

https://ally10.tistory.com/13

#2 OpenGL/C++ glm library를 사용하는 간단한 예제들

하지만 사실 이 rotate를 수행하는데에는 두 가지 방법이 있다. 오일러각과 쿼터니언.

 

 

오일러각은, xyz를 세 축을 기준으로 회전하는 것을 의미한다. 예를들어서 우리가 x축으로 10만큼, y축으로 20만큼 회전을 하고싶다고 가정해보자. 우리는 이 일련의 연산을 한꺼번에 할 수 없다. 오일러각의 정의 자체가 한 축을 기준으로 돌리는것을 의미하기 때문에, 기본적으로 x축으로 10만큼 먼저 회전하고, 그 다음에 y축으로 20만큼 회전을 할것이다.

 

어렵게 생각하기 보다는, 그냥 직관적으로 생각하면 된다. 말 그대로다.

만약 한 점 P가 이 일련의 회전 과정을 거친다고 가정해보자. 점P는 Rx에 의해 P'이 되었고, 이 P'를 다시 Ry에 의해 20만큼 회전을 시킬것이다. 이 과정을 보면 오일러각이 각 축에 대해 종속적이라는 걸 알 수 있다.

왜냐하면, 우리는 Rx를 수행한 후 Ry를 점 P에 대해 수행한게 아니라, Rx가 이미 수행된 P'에 대해서 수행했기 때문이다.

즉, 독립적으로 회전을 시킬 수 없다는 말이다. 이미 점 P'에 대해서는 x축 회전에 대한 영향이 미쳐있는 상태이다.

 

위 행렬 연산을 P*Rx*Ry가 아닌 P*Ry*Rx로 했을 때 결과가 달라지는것도 또 다른 설명이 된다.

우리가 원하는 회전 결과를 얻기 위해서는 반드시 Rx->Ry순으로 곱해져야 하며, 이는 곧 서로 dependant하다는 얘기가 된다.

 

이러한 오일러각 시스템상에, 피할 수 없는 유명한 문제점이 하나 있다.

바로 짐벌락 현상이다. 회전을 하다 보면 특정 시점에 한 축이 축 자체의 역할을 잃어버리게 되는 현상을 말한다.

 

 

빨간색은 비행기의 위아래 수직각도를 조절하는 축이고, 파란색은 좌우 비행기 시야각을 조절하는 축이고, 초록색은 비행기의 날개 각도를 조절하는 축이다. 이 그림에서 초록색 링을 한바퀴 회전시키고, 빨간링을 위쪽으로 90도 회전시킨다면 아래와 같은 회전 결과가 나온다.

 

파란축의 목적이었던 비행기 좌우 시야각을 조절하는 축이 없어져버렸다. 이게 바로 짐벌락 현상이다. 짐벌락 현상은 사실 그림으로 보면 도저히 이해가 안된다(나만 그럴수도...)

 

https://www.youtube.com/watch?v=zc8b2Jo7mno

 

짐벌락 현상과 오일러 각에 대한 설명이 잘 담긴 영상이다.

 

 

이런 문제들을 보완한게 바로 쿼터니언이다. 쿼터니언의 경우 한 축을 기준으로 해당 각도만큼 회전시킨다. 즉, 다른 축에 대한 의존성이 없다. 심지어 연산 효율도 좋다. 오일러각의 경우에는 회전시마다 9개의 행렬 원소를 필요로하지만, 쿼터니언의 경우에는 (x,y,z,w)로만 표현이 된다. 다만 쿼터니언은 오일러각에 비해 직관적이지 않아 이해하기 어렵다는게 단점이다.

 

 

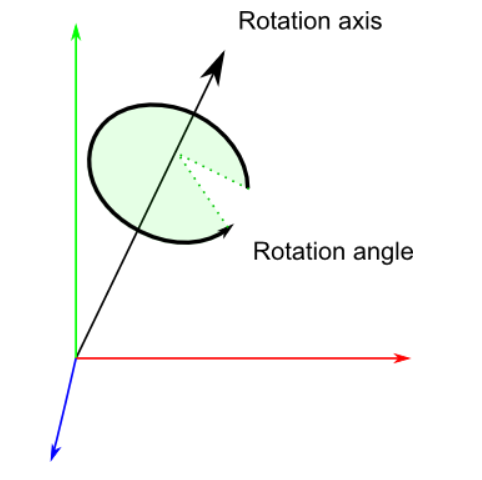
회전축인 axis를 기준으로 회전각만큼 회전변환을 한다. 또한 쿼터니언 역시 곱셈을 하면서 회전 누적이 가능하다.